

서로소 집합(Disjoint Set)
- 서로 중복 포함된 원소가 없는 집합(= 교집합이 없는 집합)들을 표현하는 자료구조이다.
- Union(합집합), Find(집합 탐색) 연산이 가능하다.
- 집합에 속한 하나의 특정 원소를 대표자라고 하며 이를 통하여 집합들을 구분할 수 있다.
이 자료구조를 Array혹은 List로 구현했을 경우 최선의 시간복잡도가 O(n + u*log(u) + f)이다.
(u와 f는 각각 Union과 Find연산이 실행된 횟수이다.)
하지만 이를 Tree로 구현할 경우 시간복잡도는 O(n + f)에 근접해진다.
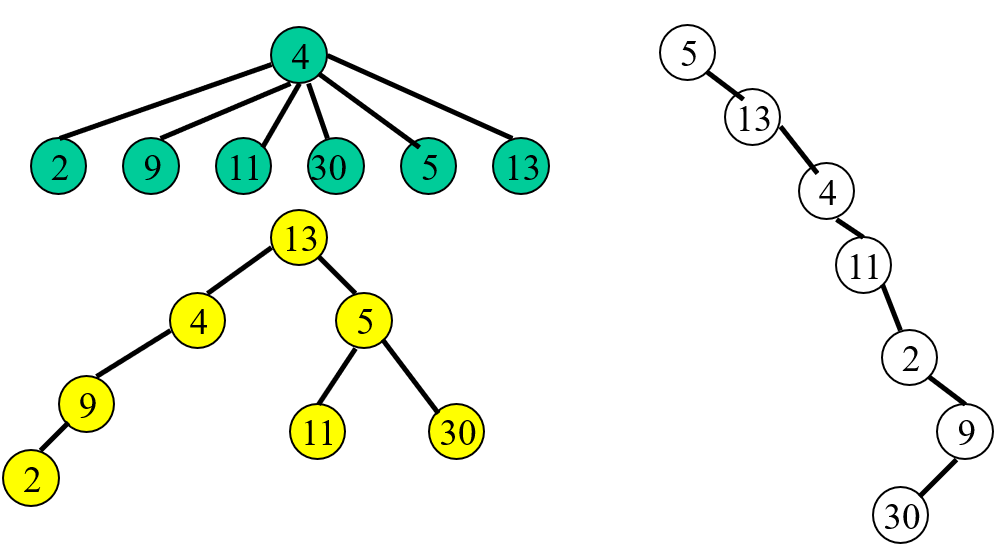
{2, 4, 5, 9, 11, 13, 30}의 원소를 가지는 집합을 트리로 표현한다면 위와 같이 다양한 모양으로 나올 수 있다.
Find 연산
Find(i)를 하게 되면 i를 포함하고 있는 집합을 얻을 수 있다. (i가 속한 Tree의 Root를 얻을 수 있다. = 대표자)
따라서 i 와 j가 같은 집합에 속해있다면, find(i)와 find(j)의 반환 값은 같다.
- 원소 i를 가지고 있는 노드에서 시작하여 루트노드에 도착할때까지 올라간다.
- 루트노드의 원소(대표자)를 반환한다.
- 트리를 오르기 위해서는 각 노드는 부모노드의 위치를 가지고 있어야한다.
그래서 각 원소의 부모노드의 원소를 저장하는 parent 배열을 하나 만든다.
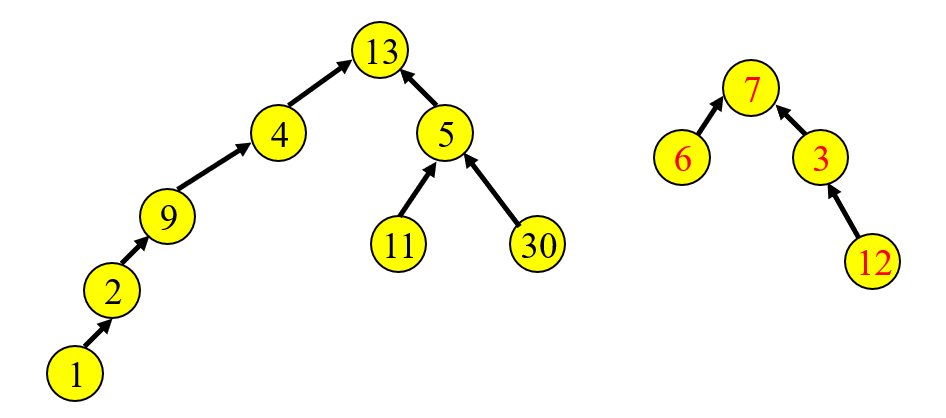

위의 사진과 같이 배열의 인덱스를 원소라고 할때 그 부모노드의 원소를 배열의 데이터로 넣는 것이다.
int SimpleFind(int i)
{
while (parent[i] > 0)
i = parent[i]; // move up the tree
return i;
}
그러면 이런 식으로 코드를 짜볼 수 있을 것이다.
find연산의 시간복잡도
맨 처음에 모든 원소가 자기 자신만을 원소로 가지는 n개의 서로소 집합으로 시작했다고 가정하면 아래 사진과 같이 Union(2,1), Union(3,2), Union(4,3), Union(5,4)를 해서 저런 길쭉한 모양의 트리가 나올 수 있다. 저런 길쭉한 모양이 나왔을때가 find의 최악의 경우의 수이다. 이때 find의 시간복잡도는 Union을 한 횟수와 같다. 따라서 Union을 실행한 횟수를 u라고 하면 find의 시간복잡도는 O(u)이다.

Union 연산
Union(i, j)
- i와 j는 서로 다른 트리의 루트여야 한다.
- 트리를 Union하기 위해선 한 트리를 다른 트리의 서브트리로 만들면 된다.
방법은 정말 간단하다. 한 트리의 루트노드의 부모노드를 다른 한 트리의 루트노드로 설정해주면 된다. 우리는 위에서 parent 배열을 만들었기 때문에
void SimpleUnion(int i, int j)
{
parent[j] = i;
}
이런식으로 정말 간단하게 만들 수 있다. SimpleUnion의 시간 복잡도는 배열 하나의 원소를 변경하는 것 이기 때문에 O(1)이라고 볼 수 있다.
그러면 u번의 Union을 수행하고 f번의 Find를 수행했을 때의 시간 복잡도는 O(u + uf) = O(uf)이고 맨처음에 parent배열의 모든 원소를 0으로 초기화 시켜주는것이 O(n)이므로 총 시간복잡도는 O(n + uf)이다. chain이나 array를 사용한다면 더욱 오래 걸릴 것이다.
Union과 Find 연산 성능 향상을 위한 방법
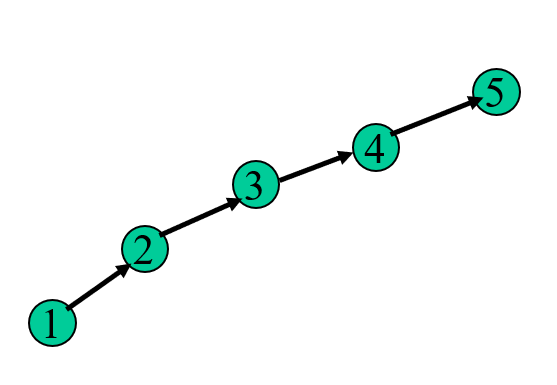
find연산을 할때, 위 그림과 같이 이런 길쭉한 모양의 tree가 많이 나온다면 find연산의 작업량이 많아질 수 밖에없다. 이런 모양의 tree가 나오는 경우를 최소화 할 수 있는 방법은 없을까? 그 해답은 union을 수행할때 어떠한 규칙에 의해서 수행한다면 그 경우를 줄일 수 있다. 이때 적용할 수 있는 규칙이 두가지가 있는데 Height Rule과 Weight Rule이다.
- Height Rule
Union을 수행할때, 낮은 height를 가지는 트리를 다른 트리의 subtree로 만드는 방법이다. 이 경우 같은 height를 가지는 두 집합을 union할때만 height가 증가한다.
- Weight Rule
Union을 수행할때, 원소의 수가 적은 트리를 다른 트리의 subtree로 만드는 방법이다. 일반적으로 원소의 갯수가 작은 것이 height가 작다는 특성을 이용해서 성능의 향상을 생각할 수 있다.
이 룰을 어떻게 적용할 수 있을까?
- 루트노드에 트리의 높이(height rule) 혹은 원소의 갯수(weight rule)를 저장해야 한다.
- height rule을 사용할 때는 같은 height를 가지는 두 집합을 union할때만 height를 1 증가시켜준다.
- weight rule을 사용할 때는 합치려는 두 트리의 원소의 갯수의 합을 root의 weight로 설정해준다.
이 규칙을 적용하게 되면 p개의 원소를 가지는 집합이 나올 수 있는 최악의 높이는 log(p) + 1이다.
따라서 log(n + uf)의 시간복잡도를 O(n + log(u)*f)로 줄일 수 있게 되었다!
여기서 성능을 더 좋게할 수 있는 방법이 존재한다.
그 방법은 find를 수행할떄, 현재 가리키고 있는 노드의 부모노드를 모두 root로 바꿔 버리는 것이다. 이러면 처음 find할때는 성능의 향상이 없겠지만 그 이후의 find를 반복하면 반복할 수록 height는 2에 가까워지고 성능향상을 도모할 수 있다.
예시를 들자면
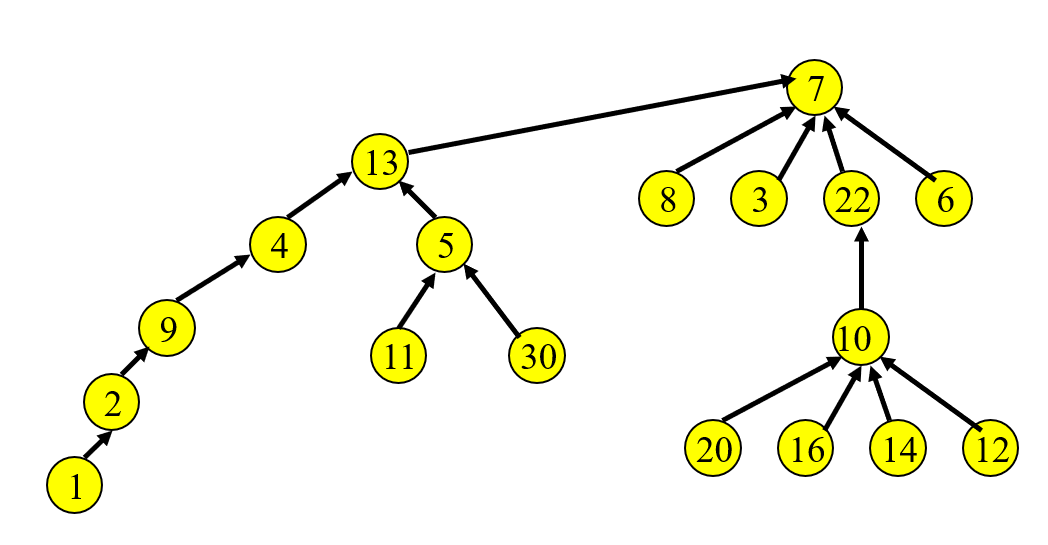
이런 트리가 있다고 할때, find(1)을 하게 되면 1 -> 2 -> 9 -> 4 -> 13 -> 7 순서로 올라가면서 7을 반환해 줄 것이다. 그런데 1을 가리킬때 1의 부모노드를 7로 바꿔주고 다음 2로 올라가서 2의 부모노드를 7로 바꾸어주고 이 과정을 반복하면

이런 트리를 만들 수 있고 find를 수행하면 수행할수록 height는 2에 가까워 질 것이고 find는 더욱 빨라질 것이다.
'CS > Data Structure' 카테고리의 다른 글
| [자료구조] 동적배열 구현하기 (0) | 2022.03.08 |
|---|---|
| [자료구조] 배열, 연결리스트 (0) | 2022.03.08 |
| 신장 트리(Spanning Tree) (0) | 2021.05.30 |
| 선택트리(Selection Tree) (0) | 2021.05.08 |
| 이진탐색트리(Binary Search Tree) (0) | 2021.05.06 |

게임개발자를 꿈꾸는 대학생의 개발 공부 블로그
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[자료구조] 배열, 연결리스트](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FWvh8R%2FbtrvrA4pqr5%2FAAAAAAAAAAAAAAAAAAAAAA96XeipER4-PoSmYHzIVD7ZPtSCn8Wa-F1sOeE-D7nY%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DviRM%252F4n598iJlK6R7J8BwkwapwM%253D)
